 |
Het Romeinse getallenstelsel
Op wiskundig vlak hebben de Romeinen niet bepaald een voortrekkersrol gespeeld. Hun getallenstelsel is waarschijnlijk ontstaan als een telsysteem voor herders, die op een kerfstok bijhielden of ze wel met al hun schapen terug thuis waren gekomen. Later evolueren de kerfstreepjes tot letters die uit het Romeinse alfabet worden overgenomen. Maar het blijft een primitief systeem. Toch wel verwonderlijk als je bedenkt welk een hoog niveau de Romeinse beschaving bereikt. Het maken van voor ons eenvoudige berekeningen als vermenigvul-digingen en delingen, is met Romeinse getallen een hopeloze opgave. Eigenlijk wordt het alleen gebruikt voor notaties en gebeuren berekeningen met een 'abacus' of rekentafel. Nochtans blijft het systeem in Europa nog tot in de Middeleeuwen algemeen in zwang.
 |
Ons getallenstelsel danken we echter aan de Arabieren, die het op hun beurt van de Indiërs hebben overgenomen. Een Spaans manuscript uit 976 is de oudste vermelding van het gebruik van de Indisch-Arabische cijfers in Europa. Via Spanje en Sicilië dringt het nieuwe systeem rond de 13e eeuw door tot in West-Europa. Het arabische systeem is veel logischer en eenvoudiger en het duurt dan ook niet lang of handelslieden, bankiers en andere mensen die veel moeten rekenen, schakelen over naar dit nieuwe getallenstelsel. De 'abacisten' moeten het afleggen tegen de 'algoristen', die rekenen met in zand geschreven cijfers. (Onze term 'algebra' stamt van het Arabische woord 'al-ghobar', het fijne stof waarmee de rekenaars hun rekenplankjes bestrooien om er cijfers in te noteren. Het woord 'algoritme' is een verbastering van de naam van de wiskundige al-Khwarizmi, die omstreeks 825 een boek schrijft over de nieuwe manier van rekenen.)
Romeinse getallen worden nog wel gebruikt voor het nummeren van de pagina's van een boek (wat we zelfs heden ten dage nog af en toe zien), of voor de notering van een datum. Op gebouwen bijvoorbeeld en tegenwoordig nog bij films, zodat je niet meteen kunt zien uit welk jaar precies een of andere oude draak stamt. Een speciaal geval vormen chronogrammen. Oorspronkelijk zijn de Romeinse cijfers kerfstreepjes. Ze zijn dus niet gebaseerd op de beginletters van woorden, zoals sommigen denken. De latere Romeinen gebruiken geen aparte karakters voor de cijfers, maar lenen een aantal letters uit het gewone alfabet. Maar in een inscriptie van omstreeks 170 vóór Christus, gevonden in het Zuid-Italiaanse Lucania, zien we voor het getal '50' nog een naar beneden wijzend pijltje in plaats van de letter L.
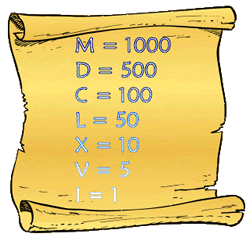
De Romeinen gebruikten volgende cijfers:
M = 1000
D = 500
C = 100
L = 50
X = 10
V = 5 (waarbij je in acht moet nemen dat ze de V en U op dezelfde manier schreven - vooral in chronogrammen speelt dat een rol) I = 1 (ook I en J schreven ze hetzelfde).
 |
De Romeinen kennen alleen maar hoofdletters (kapitalen). Maar soms vind je - bijvoorbeeld bij een paginanummering - ook wel Romeinse getallen in kleine letters. Het Romeinse systeem is ook decimaal - dus met 10 als basisgetal - maar de plaats van het cijfer in het getal heeft niet dezelfde belangrijke betekenis als in ons moderne 'positiegetallenstelsel'. Wat we bedoelen met dat laatste woord? Wel, neem het getal 777 even als voorbeeld. Daarin betekent elke 7 iets anders, afhankelijk van zijn plaats in het getal. Van rechts naar links (!) meer bepaald: 7, 70 en 700. Maar in het Romeinse getal CCC betekent elke 'C' 100.
Het Romeinse getallenstelsel is dus additief: de waarde van een romeins getal vind je door alle cijfers bij elkaar op te tellen. Bijna per definitie geven ze dus ook alleen maar gehele, positieve waarden weer. Om de noteringsvorm wat korter te maken, voegen ze later aan het systeem een subtractief element toe: als een kleinere waarde vóór een grotere staat, moet je de kleinere aftrekken.
Zo betekent
'IX': 10 - 1 = 9,
'IV': 5 - 1 = 4 en
'CM': 1000 - 100 = 900.
Alleen veelvouden van 4 en van 9 worden op die manier weergegeven. Bovendien geldt de restrictie dat alleen de combinaties IV, IX, XL, XC, CD en CM zijn toegelaten. Tenminste: zo zou het moeten zijn. In de praktijk stel je toch wel eens vast dat van deze regel wordt afgeweken. Dat geldt ook voor de regel dat je een zelfde letter nooit meer dan drie keer na elkaar mag gebruiken. 4 moet je als 'IV' noteren en niet als 'IIII'. De tweede noteringsvorm komt nochtans voor.
Wat begrijpelijk is: het is immers de oudste vorm, die door de nieuwere (IV) is verdrongen. Zeker waar het grotere getallen betreft bestaan er nogal wat afwijkende schrijfwijzen. Vier voorbeelden om dat te illusteren:
![]()
De eerste is een alternatieve schrijfwijze voor 1.000 (duizend), de tweede voor 5.000. De schrijfwijze voor 1.000 is eigenlijk een stilering van een cirkel (= twee gespiegelde C's) met een vertikale streep in het midden. Twee concentrische cirkels staan dan voor 10.000 en drie voor 100.000. (Theoretisch kun je zo nog grotere veelvouden van 1.000 weergeven. Maar in de praktijk gebeurt dat niet omdat de getalwaarde van een dergelijke notering niet goed meer in één oogopslag te lezen is.)
 |
Halve cirkels (meer bepaald de rechterkant = een I met rechts daarvan één of meer C's in spiegelschrift) geven aan dat je het zo bekomen getal door twee moet delen. (Zo kun je ook de 'D' voor 500 beschouwen als een halve duizend in deze notering.) Het derde en het vierde getal hierboven stellen respectievelijk 12.000 en 30.000.000 voor.
Het horizontale streepje geeft aan dat je het getal eronder met 1.000 moet vermenigvuldigen. Staat het getal in een niet gesloten rechthoek, dan moet je het met 100.000 vermenigvuldigen.
Zelfs combinaties zijn mogelijk: als je het 3e getal hierboven vlak achter het 4e zou schrijven, krijg je de Romeinse notering voor 30.012.000.
Dat een dergelijke schrijfwijze verwarring kan scheppen en aanleiding kan geven tot interpretatiefouten, spreekt vanzelf. Zo zou keizer Tiberius aan de latere keizer Galba ooit 500.000 in plaats van 50.000.000 sestertiën hebben uitbetaald omdat het bedrag in het legaat is aangeduid als
![]()
De streepjes aan de zijkanten zijn zo kort dat Tiberius ze niet als vertikale lijnen heeft willen zien, maar als begin- en eindpunt van de horizontale streep.
Chronogrammen
Vooral in de 17e en 18e eeuw is het gebruik van chronogrammen heel populair: het jaartal wordt verwerkt in een zin, meestal in het Latijn, die iets over de gebeurtenis zelf zegt. Om de jaartalwaarde van een chronogram te berekenen, moet je alle letters uit de zin, die een romeins cijfer zijn, bij elkaar optellen.